Odds Of 4 Of A Kind In Texas Holdem

Introduction

'Bad beat' is a term that can mean having an outstanding chance of winning a bet, only to still lose. The term can be used in any form of gambling but is most commonly applied to poker. Many poker rooms offer a progressive jackpot for very unlikely bad beats. Various other rules are added to ensure that only surprising bad beats win. Below I present tables of bad beat probabilities, starting with the most liberal rules, and ending with the most stringent. The most stringent rules, the 'Bad Beat Type 3', are the most common, in my experience.

Following are the rules for a type 1 bad beat.

1.10 Odds On the Flop in Texas Hold’em. 1.10.1 Outs; 1.10.2 Straight and Flush Draw Odds; 1.10.3 On the flop, when you have: 1.11 Odds of hitting a hand by the river from the flop. 1.11.1 On the flop, when you have: 1.12 All-in One-on-One in Texas Hold’em. 1.12.1 Preflop matchups when played to showdown: 1.13 Just-for-Fun Texas Hold’em odds. This makes the probability of drawing to a full house or four of a kind on the turn or river 0.334 and the odds are 1.99: 1. This makes drawing to a full house or four of a kind by the river about 8½ outs.

Both the bad beat and winning hand must be the best possible combination of five cards. In cases where the same hand can be created multiple ways (for example player has AK and the board shows AAKKQ) the player's hole cards will take priority.
Both the bad beat and winning hand must make use of both hole cards.
A full house must be beaten by a four of a kind or higher.

The rules for a type 2 bad beat are the same as type 1, plus any four of a kind, whether the bad beat hand or winning hand, must contain a pocket pair.

The rules for a type 3 bad beat are the same as type 2, plus a full house may not make use of a three of a kind entirely on the board.

In my experience, is the most common format for bad beat rules is type 3. The additional rule for type 3 makes very little difference, compared to type 2.

The following table shows the probability of each bad beat hand under all three types of rules. The table is based on a ten-player game in which nobody ever folds. The probabilities are for any pair of players meeting the qualifying rules. If you want to know YOUR probability of winning, you should divide the probability in the table by 10.

Bad Beat Probabilities

Bad Beat Hand	Type 1	Type 2	Type 3
Any full house	0.00203329	0.00050305	0.00049508
Full house, three 3's or higher	0.00189512	0.00046978	0.00046204
Full house, three 4's or higher	0.00175159	0.00043444	0.00042728
Full house, three 5's or higher	0.00160333	0.00039706	0.00039028
Full house, three 6's or higher	0.00144965	0.00035741	0.00035145
Full house, three 7's or higher	0.0012936	0.00031767	0.00031266
Full house, three 8's or higher	0.00113492	0.00027775	0.00027355
Full house, three 9's or higher	0.00097379	0.00023772	0.00023445
Full house, three T's or higher	0.00081113	0.00019759	0.00019503
Full house, three J's or higher	0.00064763	0.00015708	0.00015509
Full house, three Q's or higher	0.00048533	0.00011838	0.00011682
Full house, three K's or higher	0.00032561	0.00008130	0.00008033
Full house, three A's or higher	0.00016964	0.00004608	0.00004579
Full house, aces full of 3's or higher	0.00016004	0.00004350	0.00004322
Full house, aces full of 4's or higher	0.00014986	0.00004080	0.00004052
Full house, aces full of 5's or higher	0.00013898	0.00003797	0.00003763
Full house, aces full of 6's or higher	0.00012749	0.00003504	0.00003469
Full house, aces full of 7's or higher	0.00011580	0.00003233	0.00003203
Full house, aces full of 8's or higher	0.00010347	0.00002957	0.00002925
Full house, aces full of 9's or higher	0.00009067	0.00002673	0.00002645
Full house, aces full of T's or higher	0.00007714	0.00002383	0.00002359
Full house, aces full of J's or higher	0.00006286	0.00002064	0.0000204
Full house, aces full of Q's or higher	0.00004793	0.00001738	0.00001721
Full house, aces full of K's or higher	0.00003230	0.00001408	0.00001402
Any four of a kind	0.00001601	0.00001086	0.00001081
Four 3's or higher	0.00001437	0.00000996	0.00000992
Four 4's or higher	0.0000127	0.00000900	0.00000902
Four 5's or higher	0.00001099	0.00000805	0.00000804
Four 6's or higher	0.00000934	0.00000705	0.00000707
Four 7's or higher	0.0000078	0.00000613	0.00000611
Four 8's or higher	0.0000064	0.00000525	0.00000519
Four 9's or higher	0.00000519	0.00000439	0.00000435
Four T's or higher	0.00000414	0.00000359	0.00000357
Four J's or higher	0.00000317	0.00000287	0.00000285
Four Q's or higher	0.00000246	0.00000226	0.00000224
Four K's or higher	0.00000193	0.00000180	0.00000179
Four A's or higher	0.00000157	0.00000149	0.00000147
Any straight flush	0.0000012	0.00000122	0.00000121
Straight flush 6 high or higher	0.00000105	0.00000107	0.00000105
Straight flush 7 high or higher	0.00000089	0.00000091	0.00000090
Straight flush 8 high or higher	0.00000073	0.00000074	0.00000074
Straight flush 9 high or higher	0.00000056	0.00000059	0.00000058
Straight flush T high or higher	0.00000041	0.00000043	0.00000042
Straight flush J high or higher	0.00000028	0.00000027	0.00000027
Straight flush Q high or higher	0.00000012	0.00000012	0.00000012

Odds Of Getting 4 Of A Kind In Texas Hold Em

Methodology

The above tables are the result of random simulations of about 2.5 billion rounds each.

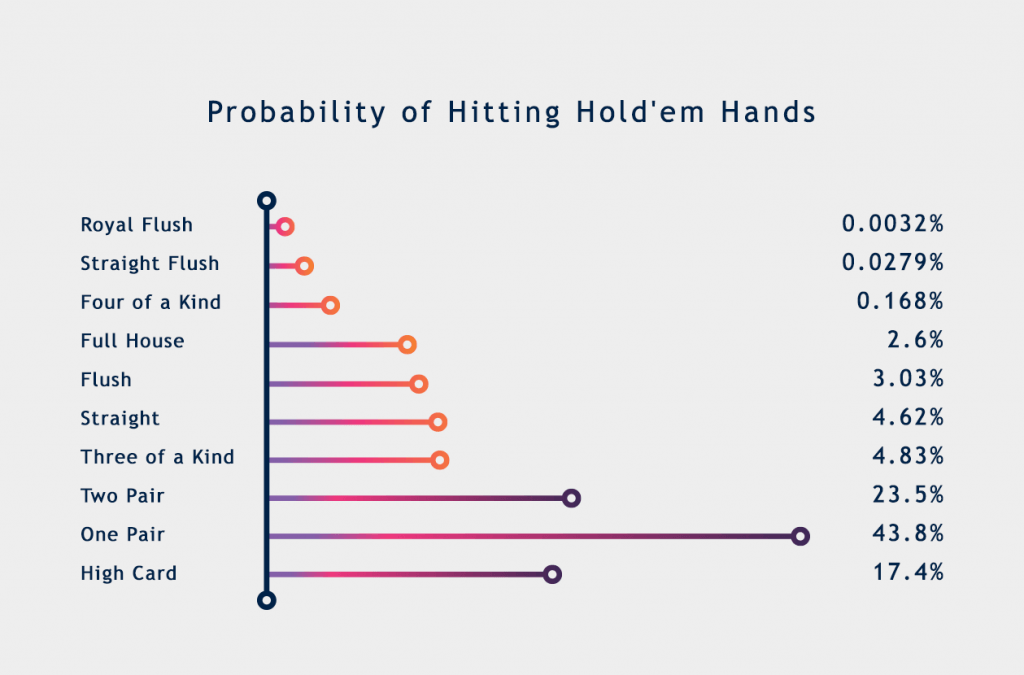
Odds Of Hitting 4 Of A Kind In Texas Holdem

There are many variations of poker, with Texas Hold ‘Em being the most popular worldwide.

Below are a whole bunch of poker facts and statistics which help you understand the chances of wining and the odds of getting the cards you want.

Did You Know?

A pocket pair is cards of the same rank, which means if your two cards have the same number, from 2-2 all the way up to A-A, this is called a pocket pair.

The odds of receiving any pocket pair is 5.9% which is 16 to 1. These are also the same odds of receiving a pocket pair of 2’s.
The odds of receiving a specific pocket pair: 0.45% or 220 to 1 These are the same odds for receiving a pocket pair of A’s.
The odds of receiving a pocket pair of A’s twice in a row is 0.002047% or 48,840 to 1.
The odds of receiving a pocket pair of K’s is 0.9% which is 220 to 1.
The odds of receiving a pocket pair of Q’s is 1.4% which is 73 to 1.
The odds of receiving a pocket pair of J’s is 1.8% which is 54 to 1.
The odds of receiving a pocket pair of 10’s is 2.3% which is 43 to 1.
The odds of receiving a pocket pair of 9’s is 2.7% which is 36 to 1.
The odds of receiving a pocket pair of 8’s is 3.2 which is 31 to 1.
The odds of receiving a pocket pair of 7’s is 3.6% which is 27 to 1.
The odds of receiving a pocket pair of 6’s is 4.1% which is 24 to 1.
The odds of receiving a pocket pair of 5’s is 4.5% which is 21 to 1.
The odds of receiving a pocket pair of 4’s is 5.0% which is 19 to 1.
The odds of receiving a pocket pair of 3’s is 5.4% which is 17 to 1.

Poker Fast Facts

Odds Of 4 Of A Kind In Texas Hold'em

The total number of possible royal flush hands in a standard 52 card deck is 4.

And the odds of making a royal flush is 649,739 to 1.

This is correct assuming that every game plays to the river.

In poker terms, the river is the name for the fifth card dealt, face-up on the board.

In total, there are 2,598,960 possible poker hands with 52 cards.

The odds of getting four of a kind in Texas Hold ‘Em is 4164 to 1.

Casinos normally change decks after 15 minutes of steady play, so that the cards can always be fresh and unmarked, as many professional players would be able to remember the certain markings on cards and use that to their advantage.

This is only a basic overview of poker odds, there are many calculators online that can help solve the odds of getting certain hands, depending on what stage of the game you’re at, what cards you currently hold and how many people are playing.

Now you are familiar with these odds, you can use them to your advantage for a better poker strategy when you finally decided to play a tournament.

In Texas Hold-Em Poker the odds of making a royal flush hand is only 649,739 to 1.

diacaveva1985.netlify.com